逻辑回归 Logistics Regression

4.1分类问题

之前的章节介绍的是如何进行线性回归的问题，本质是回归；这个章节开始介绍分类问题。最常用的回归算法是逻辑回归，就是这个标题。分类问题典型的例子是肿瘤分类，判断是良性还是恶性肿瘤；进行垃圾邮件的标记等等。分类可以分为很多种，但是最基本的是二分类。我们将因变量(dependent variable)可能属于的两个类分别称为负向类(negative class) 和正向类(positive class)，则因变量 y属于0,1 ，其中 0 表示负向类，1 表示正向类。那么如何解决呢？这里采用的是和之前有关的线性回归算法。可以假设大于1的归为1，小于0的归为0类。问题在于：线性函数的值域如如果总是在同一个区间内，例如一到正无穷那么就无法进行分类。线性回归的坏处在于输出值总有可能会超出0，1这个范围。所以逻辑回归的实质它的输出值永远在 0 到 1 之间。虽然这个算法名字是带有回归的，但是她确实可以做到分类。

4.2假说表示

对于上述的假设，我们想要的是 0 <= h𝜃(𝑥) <= 1.在这里引入了一个新的模型—逻辑回归模型 它可以令输出变量的范围始终在0，1之间。逻辑回归模型的假设是: h𝜃(𝑥) = 𝑔(𝜃𝑇𝑋) 其中: 𝑋 代表特征向量 𝑔 代表逻辑函数(logisticfunction)是一个常用的逻辑函数为 S 形函数(Sigmoid function)，就是sigmoid函数。 Python代码：

1
2
3

import numpy as np
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

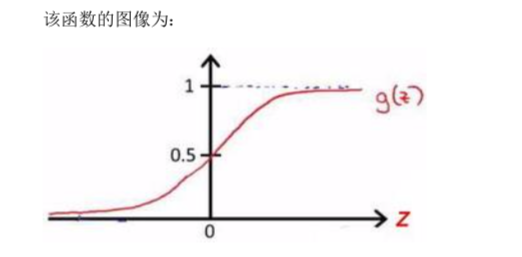
理解： h（x）的作用就是对于给定的变量，根据选择的参数计算输出变量 = 1 的可能性。

4.3决策边界

这个概念叫做decision boundary。在一个分类图像中，若是用的是逻辑回归，那么可以根据预测结果y = 1 或者 0 来分为两大类别。在图像中将这两个类别分开的边界就是决策边界。决策边界可以是一条直线，也可以是曲线。模型越复杂可能需要非常复杂的决策边界来区分不同的类别。

4.4代价函数

cost function。这个问题是根据上面的问题产生的，当我们要去拟合目标的回归模型，我们需要找到一组合适的参数θ，如何选择这个参数我们建立了选择θ的目标函数作为代价函数。在线性回归中，定义的代价函数是所有模型误差的平方和。如果将h𝜃(𝑥)带入定义的代价函数中，这个是得到的是一个非凸函数。即存在多个局部最小值，无法准确找到全局最小值。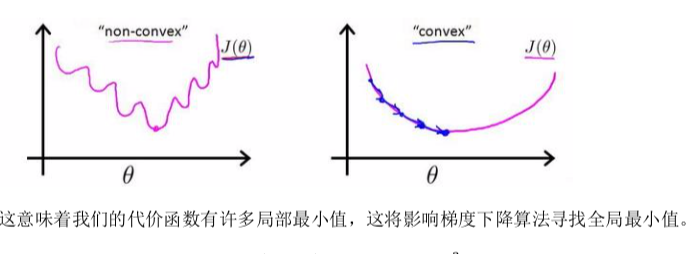我发现后面打字实在太麻烦了，直接放文字笔记吧。。。。。😓