多变量线性回归 Linear Regression with Multiple Variables
3.1多维特征
其实这个是第四节，但是上一节讲的是线性代数，都是简单的初等变换用到的知识，不用看了。
第四节从原来只有单一变量（size->price）h𝜃(𝑥) = 𝜃0 + 𝜃1𝑥 拓展到多变量，例如研究房间数，层数，房屋寿命等等对于价格的影响。
增添更多特征后，我们引入一系列新的注释:
𝑛 代表特征的数量
𝑥(𝑖)代表第 𝑖 个训练实例，是特征矩阵中的第𝑖行，是一个向量(vector)。
𝑥(𝑖)代表特征矩阵中第 𝑖 行的第 𝑗 个特征，也就是第 𝑖 个训练实例的第 𝑗 个特征。 𝑗 如上图的𝑥(2) = 3, 𝑥(2) = 2， 23 支持多变量的假设 h 表示为:h𝜃(𝑥) = 𝜃0 + 𝜃1𝑥1 + 𝜃2𝑥2+. . . +𝜃𝑛𝑥𝑛， 这个公式中有𝑛 + 1个参数和𝑛个变量，为了使得公式能够简化一些，引入𝑥0 = 1，则公 式转化为:h𝜃(𝑥) = 𝜃0𝑥0 + 𝜃1𝑥1 + 𝜃2𝑥2+. . . +𝜃𝑛𝑥𝑛 此时模型中的参数是一个𝑛 + 1维的向量，任何一个训练实例也都是𝑛 + 1维的向量，特 征矩阵𝑋的维度是 𝑚 ∗ (𝑛 + 1)。 因此公式可以简化为:h𝜃(𝑥) = 𝜃𝑇𝑋，其中上标𝑇代表矩阵转置。
3.2多变量梯度下降Gradient Descent for Multiple Variables
假设：h𝜃(𝑥)=𝜃𝑇𝑋=𝜃0+𝜃1𝑥1+𝜃2𝑥2+…+𝜃𝑛𝑥𝑛，
参数：Θ0，Θ1，Θ2，Θ3，。。。。
代价函数：平方和，即:𝐽(𝜃 , 𝜃 . . . 𝜃 ) =所有建模误差的平方和 这里就看成向量 代码示例: 计算代价函数 𝐽(𝜃)= 1 ∑𝑚 (h (𝑥(𝑖))−𝑦(𝑖))2 其中:h (𝑥)=𝜃𝑇𝑋=𝜃 𝑥 +𝜃 𝑥 + 𝜃2𝑥2+…+𝜃𝑛𝑥𝑛
化简到这里纯粹就是数学知识了，我觉得第一遍把过程搞明白以后就不用在推演了。
Python 代码:
1
2
3def computeCost(X, y, theta):
inner = np.power(((X * theta.T) - y), 2)
return np.sum(inner) / (2 * len(X))
3.3梯度下降法实践 1-特征缩放
如果特征具有相近的尺度，这将帮助梯度下降算法快速收敛。 若维度相差过大，则需要多次（非常多）迭代才能收敛。
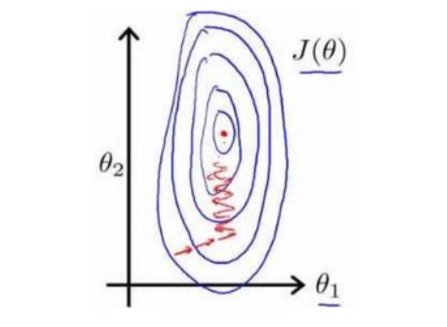
解决方法：所有特征的尺度缩放到-1<=X<=1
Feature Scaling （只要尽量保持接近就行，一般保持在（-3，3）之间）
最简单的方法均值归一化：𝑥𝑛 = （𝑥𝑛−𝜇𝑛)/𝑠𝑛，其中 𝜇𝑛是平均值，𝑠𝑛是标准差。
3.4学习率 learning rate
已经证明了α足够小的时候每次迭代后代价函数J(θ)都会下降。
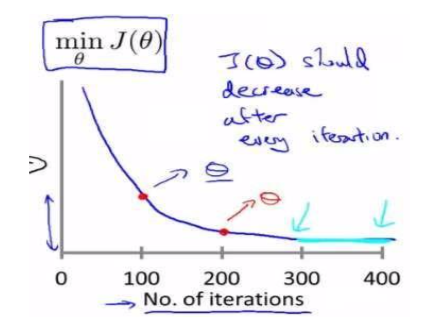总结：
α：too small 收敛太慢
α：too large 可能不会收敛甚至发散
通常可以考虑尝试些学习率:
𝛼 = 0.01，0.03，0.1，0.3，1，3，10
3.5特征和多项式回归Features and Polynomial Regression
这个问题是在实际情况中产生的，大致呈线性回归的数据是不一定严格遵守线性方程的，大部分情况是要用曲线去拟合。比如可能是三次函数的一小段等等。
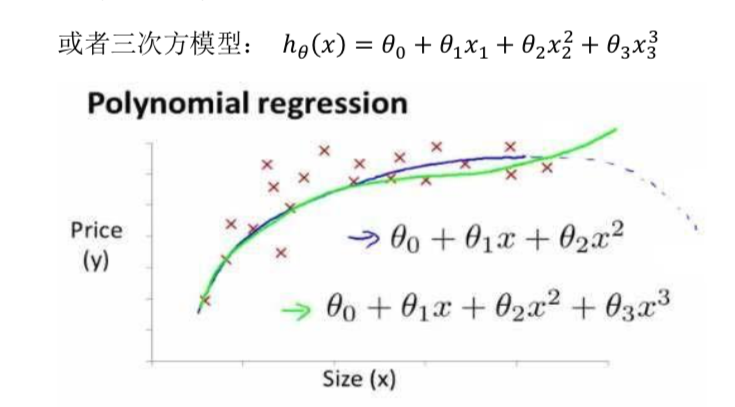采用多项式回归模型，运行梯度下降算法之前特征缩放十分重要。
3.6正规方程 Normal Equation
上述为了解决代价函数的最小值问题，采用的是梯度下降算法。但有的时候cost function使用梯度下降法太麻烦，可以直接采用求导的方式寻求使得代价函数最小的参数的。说白了就是和高中经常做的求导数等于0的极值点的问题。
这两种方法的主要区别：
梯度下降 正规方程
需要选择学习率 不需要
要多次迭代 一次计算得出
n很大时候也可以使用 n过大的时候计算代价太大 （矩阵的运算）
适用于各种模型 只适用于线性模型
这里重要的是参数θ是一个向量