单变量线性回归 Linear Regression with One Variable
2.1模型表示
明确了一些基本的定义:
- m:训练样本数
- x:特征/输入变量
- y:目标/输出值
- (x,y):训练集中实例
- (x(i),y(i))第i个观察实例 (其实这里是上标但是没法写啦
- h:学习算法/假设
这是第一个ML算法,最简单的线性回归。这里研究的是单变量,在上一张的例子中,探讨的是房屋的尺寸对于房价的影响。一般大致是房子越大房价越高嘛。这里就要研究出一个规则h,令输入的尺寸x可以得到一个y值–房价,h就是一个映射。 公式可以简单的表达为:h𝜃(𝑥) = 𝜃0 + 𝜃1𝑥。 先暂时表达为线性函数的形式。
2.2代价函数
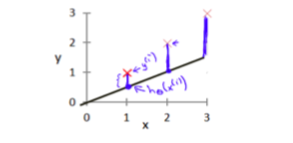
为了求得h,就要解决两个参数的取值。一般建模肯定会与实际值存在误差,当没有误差的时候那就算是成功拟合了。所以为了求的目标函数的一个方法就是最小化误差。这里就引入了代价函数。一般选取计算误差的方式使Square Error。代价函数一般用J来标记。
把𝞡0,𝞡1 和J(𝞡0,𝞡1)画到三维空间会得到一个空间中的最低点,这一个点所对应的𝞡0,𝞡1就是目标值。
在教程中有一些可视化的图片可以更加直观理解,最后的目的是得到一个自动寻找J最小的参数。
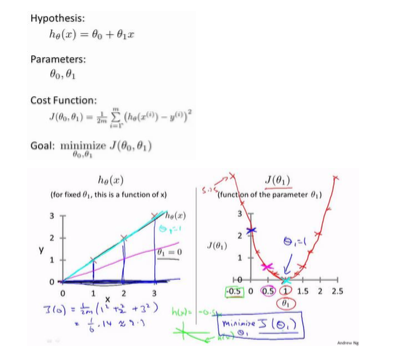
2.5梯度下降Gradient Decent
梯度下降背后的思想是:开始时我们随机选择一个参数的组合(𝜃0, 𝜃1, . . . . . . , 𝜃𝑛),计算代价函数,然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到一个局部最小值(local minimum),因为我们并没有尝试完所有的参数组合,所以不能确定我们得到的局部最小值是否便是全局最小值(global minimum),选择不同的初始参数组合,可能会找到不同的局部最小值。
这个道理和下山是一样的,如何最快从山上下来,最快的方式不是走步行道,而是从当前最陡的地方下去。每到一地就选择当前最陡的一个梯度,这样会到达一个局部的最低点。 为啥是局部的最低点呢,因为梯度为零的时候不一定是全局的最小值,这和导数为零就判断此为极大极小值是一样的问题,只能判断为局部的最大最小值,整体的还需要经过全剧验证。
批量梯度下降(batch gradient descent)算法的主要步骤:
Start with some 𝜃0,𝜃1;
keep changing 𝜃0, 𝜃1 to reduce J(𝜃0, 𝜃1);
until we hopefully end up at minimun.

在公式中𝑎是学习率(learning rate),它决定了我们沿着能让代价函数下降程度最大的方向 向下迈出的步子有多大,在批量梯度下降中,我们每一次都同时让所有的参数减去学习速率 乘以代价函数的导数。 α 这里有个细节,当在寻找新的𝜃0, 𝜃1,这两个需要同时进行更新。一般都是同步更新。这个问题老师没有解释。
2.6梯度下降的直观理解
对𝜃赋值,使得𝐽(𝜃)按梯度下降最快方向进行,一直迭代下去,最终得到局部最小值。其中α是学习率(learning rate),它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。
关于学习率: α可能会有两种情况, α太小:学习速率太小,训练次数过多,或者需要很长时间才能找到最低点。 α太大:梯度下降太大,比如下山快要到最低点了,结果步子太大跨到对面山坡上了!这样更新反而会越来越糟糕,因为会导致无法收敛。
如果一开始就在局部最低点,但是不知道却依然更新会不会出错? 不会,在次导数为零,公式中计算为𝜃0, 𝜃1 减去a*导数,这里为零那么参数也不会有变化。
这个算法有一个很巧妙的地方,当越接近局部最低点,下降幅度会越来越小,避免过大步伐导致无法收敛。 这是因为导数越来越接近0,a不变的情况下幅度自然会减小。 所以a是没有必要在最后减小的。
2.7梯度下降的线性回归
对我们之前的线性回归问题运用梯度下降法,关键在于求出代价函数的导数,这里完全就是数学问题了,么得意思。看看自己推导的笔记就完事儿了。

